Логарифмы
Свойства. Причины трудностей восприятия. О путях преодоления, и вообще, нет ли волшебной таблетки. Прямые действия и обратные — будь они неладны.
Поскольку a в степени x и логарифм x по основанию a – взаимно обратные функции, возникает впечатление о полном равноправии. Но логарифм, конечно, воспринимается
труднее. Как зубную пасту, легче выдавить из тюбика, – так и здесь, проще иметь дело с a^{x}. Ситуация ещё усугубляется тем, что вместо x=log_{a}y обычно приходится писать y=log_{a}x, меняя буквы местами, ибо этикет требует x – для аргумента, y – для функции. Если бы не это, то даже график логарифма не надо было бы рисовать заново.
Обратные функции
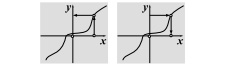
Логарифмическая функция
$y=\log_{a}x$ обратна к показательной, \[x=a^{y} ⇔ y=\log_{a}x\] Традиционно для обозначения аргумента используется буква $x$, функции – $y$. Поэтому мы пишем $x=a^{y}$, чем функцию
\[y=f(x)=\log_{a}x\]
задаём неявно. Таким образом, $y=\log_{a}x$ – это решение уравнения $x=a^{y}$ относительно $y$.
Обратные функции
Для настройки в резонанс здесь уместно
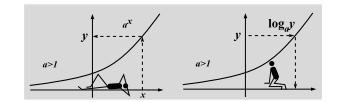
кое-что напомнить. Функция $f(x)$ – это зависимость между величинами $x$ и $y=f(x)$, причём сначала указывается $x$, затем «вычисляется» $y$. Если функция задаётся либо сопровождается графиком, то её «вычисление» $y$ сводится к построению, показанному на рисунке

слева. А определение величины $x$ по значению $y$ – изображено справа. Такая зависимость называется обратной функцией и обозначается как $f^{-1}$, т.~е.
$x=f^{-1}(y)$, но «$-1$» здесь – не показатель степени. Очевидно,
\[f(f^{-1}(z))=z; f^{-1}(f(u))=u,\] что удобнее записывать без скобок, \[ff^{-1}z=z; f^{-1}fu=u.\]
В случае экспоненты и логарифма имеем

При этом $a^{\log_{a}z}=z$; $\log_{a}a^{u}=u.$
Первое из этих тождеств $a^{\log_{a}z}=z$ называют основным тождеством для логарифмов.
Поскольку $a^{x}$ и $\log_{a}x$ – взаимно обратные функции, возникает
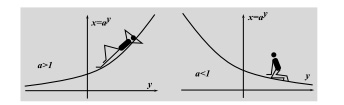
впечатление о полном равноправии. Но логарифм, конечно, воспринимается труднее. Как зубную пасту, легче выдавить из тюбика, – так и здесь, проще иметь дело с $a^{x}$. Ситуация ещё усугубляется тем, что вместо $x=\log_{a}y$ обычно приходится писать $y=\log_{a}x$, меняя буквы местами, ибо этикет требует $x$ – для аргумента, $y$ – для функции. Если бы не это, то даже график логарифма не надо было бы рисовать заново. Он уже изображен на рисунке

Правда, в обозначениях $x=\log_{a}y$ и с нестандартным расположением осей.
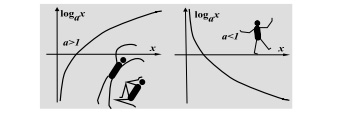
Если же буквы $x,y$ поменять местами, и оси привести в обычное положение (поворот на $90^{∘}$ плюс отражение относительно вертикальной оси), то график логарифма будет выглядеть так:

Свойства логарифмов
Таким образом, график логарифма и график показательной функции – это одна и та же кривая (с точностью до поворота и отражения). То же самое можно сказать и о свойствах этих функций. Свойства логарифма – это свойства показательной функции, выраженные на другом языке. Например, «логарифм произведения равен сумме логарифмов», \[\log_{a}bc=\log_{a}b+\log_{a}c,\] есть не что иное как $a^{β}a^{γ}=a^{β+γ}$, а \[\log_{a}b^{c}=c•\log_{a}b\] эквивалент $(a^{β})^{γ}=a^{βγ}$.
Поскольку зубную пасту вернуть в тюбик не так просто, эти элементарные правила, без привычки, даются не сразу. Видео-формат позволяет к текстовой информации добавить недостающие ингредиенты.
Далее. Логарифмируя тождество $a^{\log_{a}b}=b$ по некоторому основанию $c≠a$, получаем
\[\log_{a}b•\log_{c}a=\log_{c}b,\] откуда \[\log_{a}b={\log_{c}b}/{\log_{c}a}\] что называют формулой перехода к другому основанию. Полагая $c=b$, имеем (с учётом $\log_{b}b=1$)
\[\log_{a}b=1/{\log_{b}a}.\]
Наиболее широко распространены десятичные логарифмы и натуральные (по основанию
$e≈ 2,7$), для которых используются специфические обозначения:
\[\log_{10}x=\lg x;\log_{e}x=\ln x.\]