Числа и арифметика
О настоящих причинах введения отрицательных и дробных чисел. Как дроби помогают решать задачи с целыми числами. Что это за механизмы такие.
И на Земле, и в Раю
И на Земле, и в Раю, число есть ЧИСЛО – явление абстрактное и до некоторой степени первичное,
см. далее. О глубине понятия поначалу лучше не задумываться, дабы не раздражать Бегемотика. Ибо по идее всё просто, и с этого целесообразно начинать.
Конечно, если мы начнём умничать раньше времени, то это кому-то может
понравиться, – министру образования, например. Потому что он опасается простых разговоров, легко возбуждающих критиков. Заумное изложение – другое дело. Там критикуя, легко вляпаться. Поэтому многие воздерживаются.
Но нам-то с вами – что? Нам главное, чтобы понятно было, естественно.
Поэтому мудрить особенно не стоит. Как малых детей учат считать, так и нам подходит. Один, два, три и так далее. Порядок запоминаем, а потом убеждаемся, что процесс счёта идёт одинаково, хоть ворон считаем, хоть – учителей.
Да и арифметика трудностей не вызывает до поры до времени. Два привидения и
три обезьяны – всего пять человек}. Какие проблемы? С дробями хуже, но это отдельный разговор.
Как математики из мухи делают слона
Математики, конечно, с нами не согласятся. Не могут они на мир смотреть
по-простому. Всё у них <<с вывертом>>. Ну да ладно. Понаблюдаем, как они щёки надувают.
Итак. Сначала вводится понятие множества как совокупности своих элементов.
Элементы первичны, неопределяемы и могут быть объектами любой природы. Например,
\[S=\{1,8,3\};K=\{\Θ,\Φ,\Ω\};L=\{*,*,*\}; M=\{1,1,1\}.\]
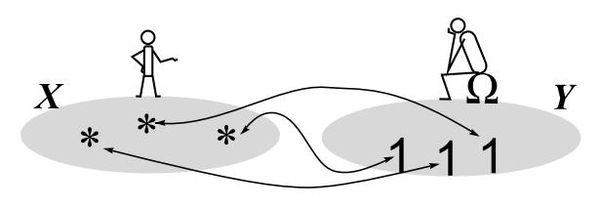
Определение. Множества $X$, $Y$ называют эквивалентными, пишут $X⊂ Y$ или
$|X|= |Y|$, если между их элементами можно установить взаимно-однозначное соответствие.
Вот пример такого соответствия. Звёздочки и единички объединяются в пары. Каждой звёздочке соответствует единичка, и наоборот.
В случае
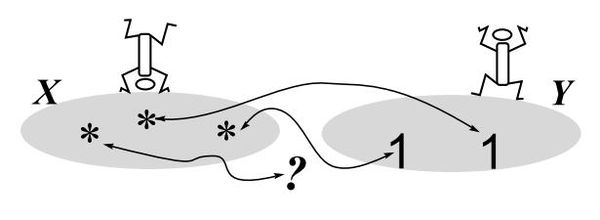
установить взаимно-однозначное соответствие не удаётся.
Отношение эквивалентности <<$∼$>> позволяет разбить все множества на классы
эквивалентности (на множества эквивалентных множеств). Класс эквивалентности множества $X$ называют его мощностью, и обозначают
как $|X|$. Множества можно упорядочить по мощности с помощью следующего трюка. Считаем множество $X$ меньше $Y$ по мощности, пишем $|X|< |Y|$, или просто $X<Y$, если взаимно-однозначное соответствие можно установить между $X$ и некоторым подмножеством $Z⊂ Y$, где в $Z$ входят не все элементы $Y$. Пока говорим о конечных множествах.
Далее в каждом классе эквивалентности выбираем по стандартному представителю – например, по множеству, элементами которого являются только
единички, и располагаем эти множества в порядке возрастания,
$$\{1\}, \{1,1\}, \{1,1,1\}, ... , \{1,... ,1\}, ...$$
Затем членам последовательности сопоставляем
какие-нибудь символы, скажем, $1,2,3,... $, и получается натуральный ряд
$$\ℕ=\{1,2,3, ... ,n, ... \},$$
члены которого называют натуральными числами.
Выглядит, конечно, наукообразно, но вопрос <<что такое число>> – получает всё же ответ. У нас-то было бу-бу-бу. Число, мол, такая штука, связанная со счётом. Какая штука? С каким счётом? Как связана? А тут
вроде концы с концами сходятся, и хвосты не повисают.
Откуда берутся отрицательные числа
Следующий шаг – отрицательные числа.
Вокруг них крутится такой водоворот глупостей, будто речь идёт о ядре Мироздания. Что это такое? Как правильно определить? Так нельзя. Ты не понимаешь. – Сам ты сибирский валенок. И так далее.
Попробуем разобраться. Будем, например, движение вправо помечать знаком плюс, <<$+$>>,
влево – минус, <<$-$>>, и тогда <<$+a$>> шагов вправо, <<$-b$>> влево, – дают в итоге результирующее местоположение $a-b=(+a)+(-b)$, что
удобно, и свидетельствует о пользе отрицательных чисел.
Критики взвиваются: детский лепет! Вспомните ещё тётю Клаву с отрицательными градусами на термометре. Мы же, дескать, в храме Математики, а не у бабы Яги на заднем дворе.
Огород городить надо абстрактно! Каждому натуральному $n$,
пишут $n∈ \ℕ$, сопоставляется <<противоположное>> число <<$-n$>> (минус $n$), называемое
отрицательным, и полагают
\[n+(-n)=n-n=0.\]
Что такое нуль, 0? – Ничто, в смысле $a-a=0$. Операция-то вычитания $a-b$ естественным образом определена в арифметике изначально при $b≤ a$. К
примеру, можно отнять часть привилегий, можно отнять – все. Поэтому к натуральному ряду имело бы смысл добавить нуль. Иногда так и делают. Но чаще в $\ℕ$ ограничиваются целыми положительными числами. Определения и терминология в жизни и в
математике нередко <<плавают>>. С этим приходится мириться, помня, что умение не переживать по поводу того, чего не можешь изменить, – это божий
дар.
В итоге натуральный ряд $\ℕ$ расширяется до множества целых чисел.
\[\ℤ=\{... ,-2,-1,0,1,2... \}.\]
При этом расширение игровой площадки $\ℕ$ до $\ℤ$ вводится для того, чтобы $b-a=b+(-a)$ никогда не уводило в аут, за пределы игровой площадки. Чтобы уравнение $a+x=b$ всегда решалось.
Множества $\ℕ$, $\ℤ$ полезно соотносить с геометрическими образами на прямой, снабжённой равномерно отстоящими делениями
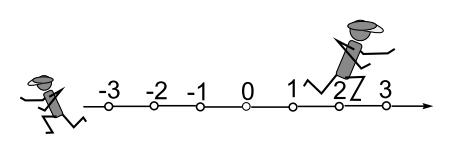
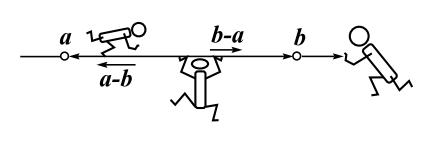
На этом поле результат вычитания можно представлять как вектор, направленный влево или вправо,
Комментарий
Первое. Сказано ли главное об отрицательных числах выше? Не совсем.
Конечно, по сути оговорено, что отрицательное число – это абстракция, выдуманный трюк, фикция. Как шахматный ферзь, выполняющий в игре определённую роль, которая никак не связана с воплощением в той или иной
форме. И это принципиальный момент. Люди обычно наделяют символические вещи
случайными атрибутами, а потом страдают от расщепления сознания. Скажем, думают об отрицательных числах как о долгах или убытках на фоне прибылей. И тогда вопрос типа <<почему $(-1)\times(-2)=+2$?>> – не получает ответа>>.
Блез Паскаль, например,
предпочитал равенства типа $0-5=0$. Ибо ему чудилось, что из <<ничто>>
сколько ни вычитай – Оно не меняется. Поэтому, какой спрос с Василя
Иваныча, который <<кровь сдал, мочу сдал, на арифметике – завалился>>. Тут выдающийся учёный, хотя и не начдив Красной армии, но тоже обойтись без тараканов в голове не сумел.
Короче, отрицательные числа – продукт игры воображения, но они, как
зеркало, способны отражать взаимоотношения реального мира. Вот так о них и надо думать, а не заземлять их на частности, оставляя в плену случайных интерпретаций.
Второе.
Отрицательные числа, разумеется, были придуманы, чтобы операция вычитания
была всегда выполнима. Проблему решает $\ℤ$, и сказке вроде бы конец. Однако расширением игровой площадки $\ℕ$ до $\ℤ$ автоматически достигнута гораздо более великая цель, что осталось за кадром. И на это надо обратить внимание.
Итак, третье, – самое главное. Играя в арифметику на той или иной
площадке, в данном случае $\ℕ$, мы сталкиваемся с тем, что <<мяч>> то и дело улетает в аут. И тогда возникает естественная идея так расширить $\ℕ$ до какого-нибудь $\ℤ$, чтобы манипулирование с числами из $ℤ$ не выводило
за пределы $\ℤ$.
В качестве $\ℤ$ мы взяли всевозможные $a± b$, где $a,b∈\ℕ$. И нам повезло, мы сразу получили игровую площадку, замкнутую по сложению и вычитанию. Могло ведь получиться, что $a± b$ для некоторых $a,b∈ \ℤ$ окажется за пределами $\ℤ$. И тогда снова пришлось бы расширять $\ℤ$. Слава богу, обошлось. В арифметике есть ещё умножение и другие операции, каковые должны
удовлетворять определённым свойствам не только на $ℕ$, но и на
расширениях. И если
мы хотим, например, иметь $x^{2}>0$ при любом $x≠ 0$, то минус на минус при
умножении должен давать плюс.
Но вернёмся к нашим баранам.
Идея расширения игровых площадок пронизывает всю математику. При этом ориентиром всегда служит замкнутость расширения по рассматриваемым
типам операций. В данном случае переход от $\ℕ$ к $\ℤ$ обеспечивает замкнутость по сложению, вычитанию и умножению. Делается это для того, чтобы потом можно было свободно обращаться с равенствами и неравенствами, упрощая их или вообще приводя к виду, удобному для тех или иных целей.
Итак, ещё раз. Множество $\ℤ$ образовалось как совокупность
разностей $a-b$ для любых $a,b∈\ℕ$. Но от такой формулировки круги по воде не расходятся. Настоящая причина целесообразности перехода к $\ℤ$ остаётся вне поля зрения. Сверхзадача в другом: надо, чтобы из
$a,b∈ \ℤ$ следовало $a± b∈ \ℤ$. Тогда складывать и вычитать на $\ℤ$ можно без опасений, что результат уйдёт за пределы $\ℤ$, т.~е. $\ℤ$ оказывается замкнутой игровой площадкой, что даёт образец, стереотип мышления, действуя по которому вводят дробные, действительные и другие числа. Кстати, расширение до замыкания по сложению множества $\{1\}$, состоящего из одной единички, приводит к $\ℕ$, а расширение до замыкания по сложению и вычитанию, даёт опять-таки $\ℤ$.}
Рациональные числа
Дроби, или рациональные числа $x=b/a$ представляют собой <<результат>> деления $b$ на $a$
для любых $a,b∈\ℤ$, исключая $a=0$. Сказано-то не слишком аккуратно. Математики бы нас засмеяли. Какой такой <<результат>>, если 5 на 7 не делится. Образуется порочный круг. Дробь $5/7$ – это результат $5:7$, а результат $5:7$ – это дробь $5/7$. Дотошные профессора тут вывернулись бы по-другому. Например, так. Если танцевать от $\ℤ$, то дробь $b/a$ – это пара чисел из $\ℤ$, где $b$ называется числителем, $a≠ 0$ – знаменателем (делителем). Дробь $b/a$ несократима, если у $a$ и $b$ нет общего делителя. Далее привели бы правила для арифметических операций с дробями.
(i) Дробь не меняется при
умножении числителя и знаменателя на одно и то же число, $b/a={bk}/{ak}, k≠0$.
(ii) Для дробей с одинаковыми знаменателями:
\[ b/a±c/a={b± c}/a;
b/a× c/a={b× c}/{a× a}; b/a:c/a= b/c.\]
И лишь потом позволили бы себе обсудить возможные интерпретации дробей. Например, как точек на прямой.
Учителя начальных классов ужаснулись бы, конечно, и мы на их стороне.
Какая там аккуратность, когда психическое здоровье малышни может пострадать. Жизнь вообще не очень аккуратна. Приблизительна, так сказать. Учимся неточно, потом выруливаем из заблуждений, будь они неладны. Математиков же учат скрупулёзно, тщательно. Из них в итоге такие умники вырастают, что они по умственным лабиринтам ужом проползают, чтобы добиться ощущения полёта орла.
Что касается правил (i), (ii), то их вроде маловато, но во
взаимодействии они остальное исчерпывают. Свойство (i) любые дроби $b/a$, $p/q$ позволяет перевести в эквивалентные с равными
знаменателями $b/a={bq}/{aq}$, $p/q={pa}/{aq}$,
после чего любой вопрос решается указанным выше способом.
Совокупность всевозможных дробей $b/a$, где $a,b∈\ℤ$,
$a≠0$, называют множеством (полем) $\ℚ$ рациональных чисел. В $\ℚ$, понятное дело, разрешимо любое уравнение
\[a• x=b, a≠0.\]
Решением служит $x={b}/a$, причём уравнение $a• x=b$
оказывается разрешимым и для дробных $a$ и $b$. Могло быть хуже. Инкарнация дробей, как решений $a• x=b$ при целых $a$ и $b$, могла бы не
обеспечить разрешимости $a• x=b$ для дробных $a$ и $b$. И это в
некотором роде была бы катастрофа. Пришлось бы вводить новые числа: сначала дроби, потом дроби дробей и т. д. Нам опять повезло – не потребовалось. Да ещё оказалось
\[λ{b}/a+μ{p}/q∈ \ℚ, λ,μ∈\ℚ.\]
Иначе говоря, множество
рациональных чисел (дробей), обозначаемое символом $\ℚ$, замкнуто в арифметике, т. е. относительно арифметических операций.
Корни целой степени
Корень квадратный из $b$ – это некое $x$, которое при возведении в квадрат даёт $b$, т.~е. $x^2=b$. Возжелав по этой причине разрешимости уравнения $x^2=b$ при любом $b∈\ℕ$, мы сталкиваемся с необходимостью расширения $\ℚ$. Дробей не хватает. Приходится добавлять иррациональные числа, но как? Решением $x^2=4$ является $x=2=√4$. Но что если $x^2=5$? Может быть найдётся несократимая дробь $b/a=√5$? Не найдётся.
Из $b/a=√5$ следует $b^2=5a^2$, откуда вытекает, что $b^2$ делится на 5, а значит и на 25, но тогда $a$ делится на 5, что противоречит несократимости $b/a$.
Поэтому при желании располагать решениями уравнения $x^2=b$ квадратные корни $√b$ приходится добавить к полю $\ℚ$ рациональных чисел. Но вот с замкнутостью в арифметике выходит загвоздка, $√2+√3$ не является корнем из какого-либо $p$, а добавление к $\ℚ$ всевозможных сумм $√a+√b$ не даёт замкнутости, поскольку $√2+√3+√5$, например, не представимо в виде $√a+√b$. Поэтому с иррациональностями не всё так просто, и вопрос имеет смысл отложить. Интересно, что «двумерные» числа $a+b√3$ с рациональными $a,b$ образуют замкнутую арифметическую площадку(проверьте). Такую же удобную площадку образуют и числа вида $a+b√{-3}$, если, не мудрствуя лукаво, считать $(√{-3})^2=-3$.
Бьющий по мозгам пример
Очень важно понимать, что «числа» из всяких «расширений» упрощают жизнь и
наращивают инструментальные возможности. Вот простенькая иллюстрация.
Рассмотрим числовой ряд
\[1,\;1,\;3,\;5,\;11,\;21,\;...\]
устроенный по правилу
\[s_{n+2}=s_{n+1}+2s_{n}.\]
Поиск $n$-го члена в виде $s_{n}=x^{n}$ после подстановки в $s_{n+2}=s_{n+1}+2s_{n}$
даёт $x^{n+2}-x^{n+1}-2x^{n}=0$, что после сокращения на $x^{n}$ приводит к необходимости решения квадратного уравнения
\[x^{2}-x-2=0,\]
корни которого $x_1=2$, $x_2=-1$. Поэтому закону
$s_{n+2}=s_{n+1}+2s_{n}$ удовлетворяет как $s_{n}=x_1^n$, так и $s_{n}=x_2^{n}$, а также их линейная комбинация
\[s_{n}=α x_{1}^{n}+β x_{2}^{n}\]
при любых $α$ и $β$. Выбирая $α$ и $β$ из условия
$s_{1}=s_{2}=1$, получаем
\[s_{n}={2^{n}-(-1)^{n}}/3.\]
Обратим внимание, что $1,\;1,\;3,\;5,\;11,\;21,\;...$ содержит только числа натурального
ряда. А вот искомая формула включает и отрицательные числа, и дроби. И без «расширений» вообще не могла быть найденной.
Десятичные дроби
Особая роль десятичных дробей связана с тем, что мы пользуемся десятичной
позиционной системой записи целых чисел, с помощью 10 цифр $a_{j}∈\{0,\:1,\:2,\:3,\:4,\:5,\:6,\:7,\:8,\:9\}$,
\[a_{n}... a_{1}a_{0}=a_{n}•10^{n}+•••+a_{1}•10+a_{0}.\]
Расширение этой идеи на дробные числа приводит к суммам
\[a_{n}•10^{n}+•••+a_{1}•10+a_{0}+\ov{b_{1}•10^{-1}+b_{2}•10^{-2}+•••},\]
которые в позиционном виде записываются как
\[a_{n}... a_{1}a_{0},b_{1}b_{2},...,\]
т.~е. коэффициенты дробной, с чертой, части
располагаются после запятой. Например,
\[2,371=2{371}/{1000}=2+3/{10}+7/{100}+1/{1000}.\]
Чтобы дробь $ p/q$ перевести в десятичную, достаточно $p$ разделить на
$q$ столбиком. Допустим, соседка попросила разделить ей 2 на 3. Тут проще разделить, чем объяснять, что не хочется.
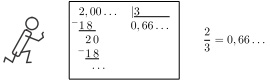
Дробь $0,77...$ периодическая – семёрки всё время повторяются, – это записывают ещё
так: 0,(7), и говорят «ноль целых и 7 в периоде».
Когда $p$ делится на $q$ столбиком, остатки в процессе вычитания, само собой,
$<q$, и потому на каком-то шаге получается тот же самый остаток, и тогда вычисления повторяются, возникает период – он может быть любой длины $<q$.
Вещественные числа
Если о целых числах думать как о делениях на прямой, то числа с точками
начинают перекликаться, и в голове возникает удобный геометрический образ. Идея стартует от представления целых чисел,
а далее сопоставляет точкам между делениями дроби $p/q$, каковых для непрерывного заполнения прямой, естественно, не хватает. Скажем, где на прямой точка $√2$, не совпадающая ни с одной дробью? Корню из 2 отвечает бесконечная десятичная дробь \[√2=1,414213562373...,\] получаемая применением вычислительного алгоритма извлечения корня, и ей можно сопоставить точку на прямой, к которой в пределе приближается следующая процедура. Отрезок $[1,2]$ делим на 10 равных сегментов. Правый конец 4-го сегмента отвечает числу $1,4$. Затем 5-й сегмент делим на 10 равных подсегментов, конец 1-го подсегмента отвечает числу $1,41$ и т.~д.
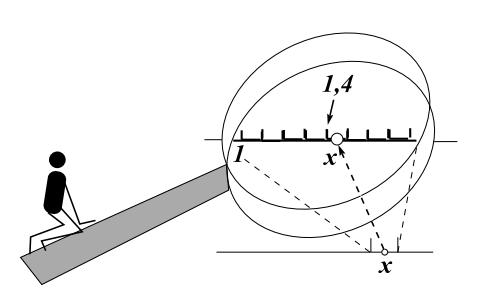
Такого сорта процедура любой конечной или бесконечной десятичной дроби
сопоставляет точку. И наоборот, любой точке – дробь.
Бесконечные десятичные дроби называют
вещественными числами, а совокупность таких чисел называют вещественной прямой, и обозначают её как $\ℝ$, или $(-\∞,\∞)$. Арифметические операции на $\ℝ$ по свойствам совпадают с аналогичными операциями на множестве рациональных чисел $\ℚ$.
Конечно, кое-что здесь требует уточнения. Особенно с точки зрения тех, кто
«перестал понимать простые вещи». В пятом-то классе им всё было ясно. Но потом начинают чудиться всякие подводные рифы, и возникает аллергия на логические неточности. Но всему своё время, в том числе – аллергии. Так что оставим пока понятие вещественного числа в обозначенном приблизительном
состоянии.