Предварительный разговор
Как лучше настроиться на изучение геометрии. На что обратить внимание.
На фоне алгебры геометрия хорошо смотрится и легко воспринимается. Конечно, когда дело доходит до всяких стереометрических фокусов, там бациллы пространственного кретинизма подтачивают планиметрическое блаженство, — но это уже другая история.
О простейших фигурах все наслышаны с детского сада.
Округлые формы, конечно, более притягательны, но и угловатые
объекты иногда завораживают. Эпизодически — сложностью, но чаще всего — простотой. Поскольку всякая успешная наука тяготеет к изучению корней, имеет смысл концентрироваться на «атомах» визуального и тактильного мира. На азбучных телах, из которых Создатель конструировал всё сущее.
Границы тел обычно представляют собой поверхности.
Граница шара есть сфера . Поверхностями называют также границы бесконечных областей (тел), а также куски поверхностей. Вот, например, обезьянье седло,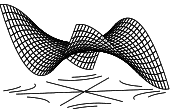 
обеспечивающее обезьяне, в отличие от обычного седла, три углубления: два для ног и третье для хвоста. Поверхности, ясное дело, встречаются сколь угодно замысловатые. Вот не самый плохой вариант — и то любопытные набежали.
обеспечивающее обезьяне, в отличие от обычного седла, три углубления: два для ног и третье для хвоста. Поверхности, ясное дело, встречаются сколь угодно замысловатые. Вот не самый плохой вариант — и то любопытные набежали.О задачах на прицеле
Приступая к изучению геометрии важно оседлать волну, с которой видны хоть какие-то горизонты. Чтобы в начале пути не возникало впечатления о переливании из пустого в порожнее. По большому счёту, конечно, куда ведёт дальний путь, – никогда не знаешь. Но какую-то перспективу имеет смысл нарисовать, дабы она согревала на скучных этапах изучения основ.
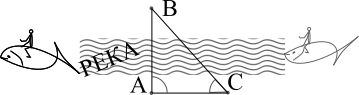
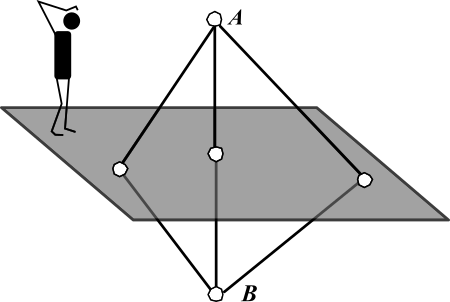
Чтобы оценить полезность геометрии, не надо даже слишком далеко заглядывать. Достаточно оглянуться вокруг. Технические чертежи, архитектура, раскрой материала, площади, объёмы, – везде требуются вычисления и другие манипуляции. Измерению-то не всё поддаётся. Скажем, точку B из A «видит око, да зуб неймёт» – река мешает. Рулетку от A до B не натянешь. Как оценить AB?
Достаточно найти доступную точку C на своём берегу, измерить AC и углы ∠A, ∠C, после чего AB легко определяется решением треугольника ABC.
Физические приложения
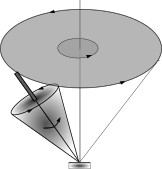
Физика без геометрии шагу ступить не может. Почти любая задача сталкивается с необходимостью изучения геометрических моделей. Пусть, например, речь идёт о движении волчка. Задача, кстати, очень сложная. Но решать её вовсе не требуется, дабы понять, что начинать тут необходимо с геометрического описания.
Скатывается ли шайба по сфере или что-нибудь — по наклонной плоскости, или подтягивается верёвкой лодка к берегу, или что угодно, — везде возникают геометрические представления, дающие возможность эффективно мыслить и вычислять.
Заколдованный круг
В силу своей наглядности геометрия выявляет подноготную, каковая в других дисциплинах остаётся в той или иной степени замаскированной. Речь идёт о том, что многие геометрические понятия, которыми мы пользуемся, при ближайшем рассмотрении оказываются «размытыми». И получается, что мы лихо манипулируем терминами, хотя, если вдуматься, за кадром остаётся много безответных вопросов. Скажем, что такое плоскость – с одной стороны, ясно. Но выразить своё понимание не так просто. Ровная поверхность? Так это эмоции. А как определить строго? Вариантов в голову приходит много. Например, плоскость можно определить как геометрическое место точек равноудалённых от некоторых данных точек A и B.
Но для этого надо предварительно определить точку, прямую и расстояние. В то же время прямую было бы удобно определить как пересечение плоскостей, а точку – как пересечение прямых. При этом, правда, возникает порочный круг, X определяется через Y , а Y – через X.
Но тут проблем (точек опоры) ещё больше. Не спасает также попытка идти от простого к сложному. Линия, мол, это след от движения точки. И так далее. «География» мысленного пути, конечно, меняется, однако заколдованный круг сохраняется. Разве что в замкнутую цепь встраиваются новые звенья.
Поэтому в любом случае приходится круг разрывать, и начинать с чего-то неопределяемого. С первичных понятий и аксиом. Точки, прямые, плоскости, — геометрия не определяет. И это следует особо подчеркнуть, сделать ударение. Идею необходимо осознать. Любая теория может стоять только на каких-то первичных неопределяемых понятиях. Разумеется, дабы А и Б определить, можно сделать шаг назад и определить А и Б через что-нибудь другое. Можно ещё сделать шаг назад, ещё, — но пятиться без конца невозможно, где-то надо остановиться.