Что такое функция
Способы задания. Характерные особенности. Коротко, — чтобы не наговорить лишнего.
90\% жизни уходит на приготовления.
\[y=f(x).\]
Другими словами, $y=f(x)$ – это зависимость $y$ от $x$. При этом переменные $x$, $y$ называют, соответственно, аргументом и функцией. Дабы общность не
парализовала наше воображение, начнём с примеров. Большей частью встречаются числовые функции. Скажем, второй закон Ньютона $$F=m• w,$$ даёт зависимость силы $F$ от ускорения $w$. Разумеется, если речь идёт о движении фиксированной массы $m$. В противном случае на $F$ можно смотреть как на функцию двух переменных $m$ и $w$.
Аналогичным образом можно взглянуть на закон Ома, Бойля–Мариотта, и вообще на различные физические взаимосвязи. Вот, например,
квадратичная функция $h$ от $t$, фиксирующая зависимость от времени высоты подъёма тела брошенного вверх со скоростью $V_{0}$:
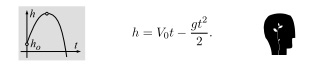
Физика здесь, конечно, сбоку бантик. Содержательная начинка необязательна.
Зависимость $y$ от $x$ можно задавать чисто формульно, алгоритмически: \[y=x^{2}-3,\qquad y=\bfrac{2x+5}{x^{2}-1}.\]
Графическое представление функции
Удобный способ описания числовой функции – графический. На плоскости
берём две взаимно перпендикулярных линии, градуируем их, одну – называем осью иксов, другую – осью игреков. Тогда на плоскости зависимости $y=f(x)$ отвечает множество точек (пар чисел) $\{x,f(x)\}$, называемое графиком $f(x)$,
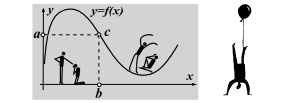
Таким образом, график функции является её геометрическим представлением,
чрезвычайно популярным из-за визуальной наглядности. В то же время, наоборот, график может служить способом задания функции. Рисуем график, и тогда игреки «вычисляются» с помощью геометрического построения. Из любой точки $x=b$ восстанавливаем перпендикуляр к оси $x$ до
пересечения с графиком в точке $c$, затем из $c$ опускаем перпендикуляр на ось $y$, получаем значение функции $y=a$.
Характерные особенности
Имея дело с функциями, желательно уметь их классифицировать и характеризовать. Важный
класс образуют непрерывные функции, у
которых малым изменениям аргумента отвечают малые изменения функции. Это не совсем точное определение, но мы тут не будем бежать впереди
паровоза, – что увело бы нас далеко в сторону. Интуитивно функцию считают непрерывной, если её график можно нарисовать, не отрывая
карандаша от бумаги. Такое «определение» высмеивают в Высшей Школе, но на первых порах оно вполне удовлетворительно. «Берега» обозначают ситуации в
которых непрерывность отсутствует, функция терпит разрывы. Вот два примера.
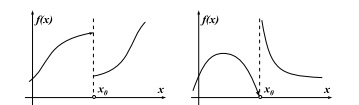
Множество тех $x$, для которых значения $f(x)$ определены, называется областью определения функции $f$. Для функции
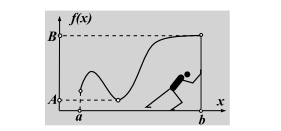
областью определения служит отрезок $[a,b]$, а областью её значений – отрезок $[A,B]$.
Точки $x$, в которых $f(x)=0$, называются корнями функции. На нижеследующем рисунке это точка $x=c$. В точках $x=a$ и $x=b$ на
том же рисунке функция принимает локально максимальное и локально минимальное значение. Локальный минимум в точке $x=b$ не является глобальным.
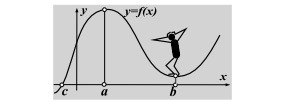
Если $f$ разные точки $u≠ v$ переводит в разные точки ${f(u)≠ f(v)}$,
то функция $f$ обратима, взаимнооднозначна. Обратную функцию обозначают как $f^{-1}$, но «$-1$» здесь не является показателем степени. Если, например, $f(x)=x^{3}$, то $f^{-1}(x)=∛{x}$, поскольку
\[y=x^{3}⇒ x=∛{y}.\]
Взаимную однозначность функции обеспечивает её
монотонность. Функция $f(x)$ называется
монотонно возрастающей, если из
$u>v$ следует ${f(u)≥ f(v)}$, и – строго возрастающей, если ${f(u)>f(v)}$. В случае монотонного убывания – ${f(u)≤ f(v)}$. На рисунке
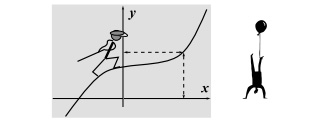
изображена монотонно возрастающая функция.